Vertex Transformation Pipeline: Local to Screen Space
Below is a concise documentation on the vertex transformation pipeline from local space to screen space, covering the model, view, and projection stages, including the handling of complex hierarchical transformations (e.g., when an object has a parent that is rotated and translated):
The vertex transformation pipeline converts 3D vertex data defined in an object's local space into 2D screen coordinates. This process is generally broken into several key stages: Model Transformation, View Transformation, Projection Transformation, and Screen Space Mapping.
-
Pipeline Overview:
The vertex transformation pipeline involves converting an object's vertex data from its local coordinate space into world space using the model transformation. Then, the view transformation repositions the scene relative to the camera. Next, the projection transformation maps the view-space coordinates to clip space, which are then converted to normalized device coordinates and finally mapped to screen space. -
Key Concepts:
- Matrix Multiplication:
Sequential transformations are applied by multiplying the appropriate matrices. - Hierarchical Transformations:
Objects with parent-child relationships require combining the parent's and child's transformations. - Perspective Divide & Viewport Mapping:
The perspective divide normalizes coordinates, and the viewport transform adapts these to the actual screen dimensions.
- Matrix Multiplication:
Note : Some images are from codinglabs
See these links for more info :
- http://www.codinglabs.net/article_world_view_projection_matrix.aspx
- https://webgpufundamentals.org/webgpu/lessons/webgpu-perspective-projection.html
- https://eater.net/quaternions
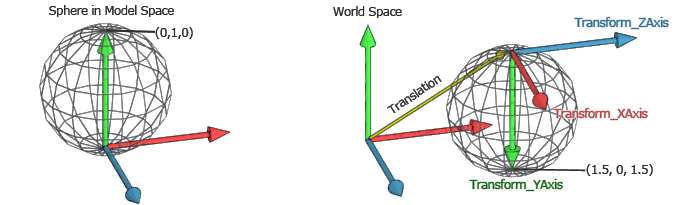
1. Model Transformation (Local to World Space)
Space conversion :
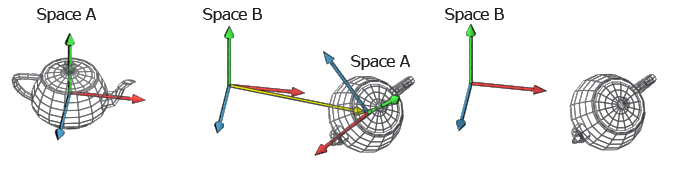 From model to world space
From model to world space
-
Purpose:
Transform vertices from the object's local coordinate system to the world coordinate system. -
Hierarchical Transformations:
When an object is part of a hierarchy (for example, a child object with a parent that is rotated or translated), the local transformation matrix of the child is combined with the parent's world transformation matrix. This results in a composite transformation that correctly positions, rotates, and scales the child relative to the global scene. These common transformations (translate, rotate, scale) are first done using Quaternions and Vectors in Transform (worldPosition and worldRotation) and then converted into a matrix in RenderEngineUtility.toModelMatrix -
Mathematical Representation:
The final world transformation for a vertex is computed as:mat4 modelMatrix = parentWorldMatrix * childLocalMatrix; vec4 worldPosition = modelMatrix * vec4(localPosition, 1.0);Here, each transformation is represented as a 4×4 matrix, and the vertex is extended to homogeneous coordinates.
2. View Transformation (World to View Space)
From world to view space
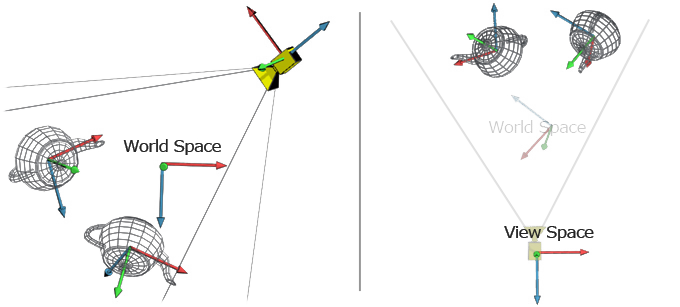
On the Left two teapots and a camera in World Space; On the right everything is transformed into View Space (World Space is represented only to help visualize the transformation)
-
Purpose:
Convert world space coordinates into view (or camera) space coordinates. This positions the scene relative to the camera. -
Concept:
The view matrix is typically the inverse of the camera's transformation matrix (position and orientation). It repositions the scene so that the camera is effectively at the origin, looking down the negative Z-axis. -
Mathematical Representation:
vec4 viewPosition = viewMatrix * worldPosition;
3. Projection Transformation (View Space to Clip Space)
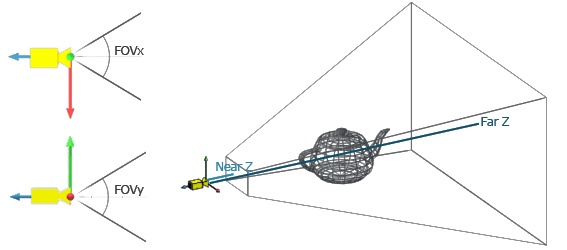 Perspective projection :
Perspective projection :
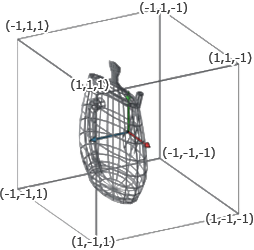
-
Purpose:
Project 3D coordinates into a 2D plane, preparing them for rasterization. -
Types of Projections:
- Perspective Projection:
Simulates realistic depth by making objects farther from the camera appear smaller. This projection is defined by the field of view (FOV), aspect ratio, and near/far clipping planes. - Orthographic Projection:
Projects vertices with uniform scaling regardless of depth, often used for UI elements or 2D renderings.
- Perspective Projection:
-
Mathematical Representation:
vec4 clipPosition = projectionMatrix * viewPosition;
4. Screen Space Transformation (Clip Space to Screen Space)
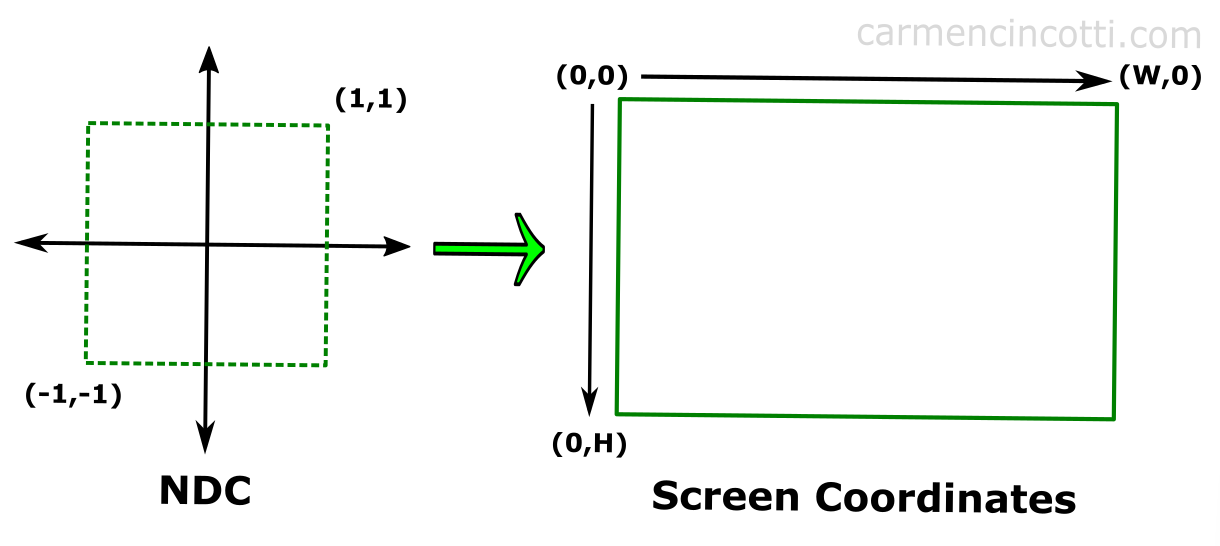
-
Purpose:
Convert the clip space coordinates into screen space coordinates that correspond to actual pixel positions on the display. -
Steps:
- Perspective Divide:
Convert from homogeneous clip space to normalized device coordinates (NDC) by dividing by the w-component.vec3 ndcPosition = clipPosition.xyz / clipPosition.w; - Viewport Transformation:
Map the NDC (usually in the range [-1, 1]) to window or screen coordinates based on the viewport dimensions.vec2 screenPosition; screenPosition.x = (ndcPosition.x * 0.5 + 0.5) * viewportWidth; screenPosition.y = (ndcPosition.y * 0.5 + 0.5) * viewportHeight;
- Perspective Divide: