The original version of this article on the Separating Axis Theorem (SAT) can be found on dyn4j.
Overview of the Separating Axis Theorem (SAT)
The Separating Axis Theorem (SAT) is a method for determining whether two convex shapes are intersecting. In addition to detecting collisions, SAT can calculate the minimum penetration vector, which is particularly useful for physics simulations and other applications. SAT is a versatile and efficient algorithm that eliminates the need for collision detection code specific to each shape pair, simplifying code maintenance and reducing complexity.
Concept of Convexity
SAT applies exclusively to convex shapes. A shape is defined as convex if any line drawn through it intersects the shape at most twice. Conversely, if a line can intersect the shape more than twice, the shape is classified as non-convex (or concave). For formal definitions, refer to Wikipedia or MathWorld.
Examples of Convexity
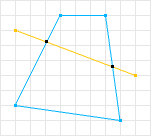
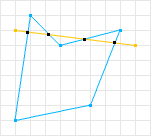
In Figure 1, the shape is convex as no line can intersect the shape more than twice. In contrast, Figure 2 illustrates a non-convex shape where such intersections exist.
SAT can only operate on convex shapes. However, non-convex shapes can be represented as combinations of convex shapes through a process called convex decomposition. For example, the non-convex shape in Figure 2 can be decomposed into two convex shapes, as shown in Figure 3. Testing each resulting convex shape individually allows for collision detection of the original non-convex shape.
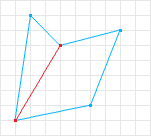
Figure 3: A convex decomposition
The Concept of Projection
Projection is a key concept in SAT. It involves creating a "shadow" of an object onto a surface when exposed to a light source with parallel rays. For a two-dimensional object, this "shadow" becomes a one-dimensional projection.
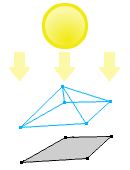
Figure 4: A projection (or shadow)
The Separating Axis Theorem
The Separating Axis Theorem states:
"If two convex objects are not intersecting, there exists at least one axis along which their projections do not overlap."
Identifying No Intersection
To determine that two shapes are not intersecting, the algorithm identifies an axis—known as the separation axis—where their projections do not overlap.
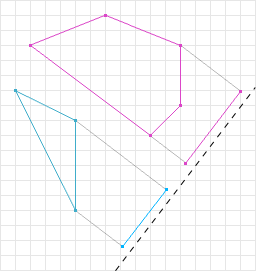
In Figure 5, two shapes are separated, and a line is drawn to illustrate this separation. When the shapes are projected onto an axis perpendicular to this line, as shown in Figure 6, their projections do not overlap. This indicates that the shapes are not intersecting.
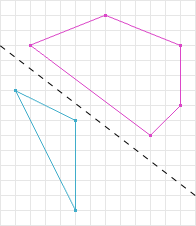
- Figure 5: Two separated convex shapes
- Figure 6: Projections of separated convex shapes
SAT performs multiple axis tests and can terminate early upon finding a separation axis, making it highly efficient for scenarios involving numerous objects but few collisions (e.g., games and simulations).
Identifying Intersection
If projections on all tested axes overlap, the algorithm concludes that the shapes are intersecting. Figure 7 demonstrates two intersecting convex shapes where projections on all axes overlap.
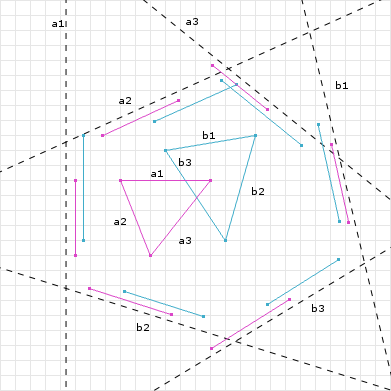
Figure 7: Two intersecting convex shapes
For SAT to confirm an intersection, all axes must be tested, and projections must overlap on every axis.
Obtaining Separation Axes
The axes to test are derived from the normals of the edges of each shape. Normals can be calculated by flipping the coordinates of an edge and negating one of them. This process generates two lists of axes, one for each shape, which are used for testing.
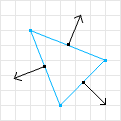
Figure 8: Edge normals
Projecting a Shape onto an Axis
To project a polygon onto an axis:
- Iterate through all vertices of the shape.
- Perform the dot product between each vertex and the axis.
- Record the minimum and maximum values to represent the projection range.
This straightforward calculation is repeated for each axis during the SAT testing process.